Graphs and Symmetry

  1. Symmetry (Geometry)

    Definition

    We say that a graph is symmetric with respect to the y axis if for every point (a,b) on the graph, there is also a point (-a,b) on the graph.

      
    Visually we have that the y axis acts as a mirror for the graph.  We will demonstrate several functions to test for symmetry graphically using the graphing calculator.


      

    Definition

    We say that a graph is symmetric with respect to the x axis if for every point (a,b) on the graph, there is also a point (a,-b) on the graph.


    Visually we have that the x axis acts as a mirror for the graph.  We will demonstrate several functions to test for symmetry graphically using the graphing calculator.  


    Definition

    We say that a graph is symmetric with respect to the origin if for every point (a,b) on the graph, there is also a point (-a,-b) on the graph.  


    Visually we have that given a point P on the graph if we draw a line segment PQ through P and the origin such that the origin is the midpoint of PQ, then Q is also on the graph.  




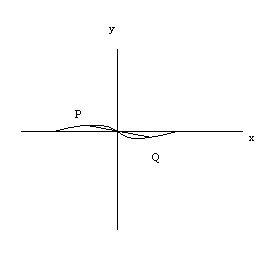
    We will use the graphing calculator to test for all three symmetries.


  2. Symmetry (Algebra)

     

    Examples:  

    1. x-axis Symmetry

       To test algebraically if a graph is symmetric with respect the x axis, we replace all the y's with -y and see if we get an equivalent expression.  

      1. For 

                x - 2y = 5 

        we replace with 

                x - 2(-y) = 5

        Simplifying we get

                x + 2y = 5 

        which is not equivalent to the original expression.

      2. For 

                x3 - y2 = 2 

        we replace with   

                x3 - (-y)2 = 2 

        which is equivalent to the original expression, so that 

                x3 - y2 = 2 

        is symmetric with respect to the x axis.

    2. y-axis Symmetry

       To test algebraically if a graph is symmetric with respect to the y axis, we replace all the x's with -x and see if we get an equivalent expression.

      1. For 

                y = x2  

        we replace with 

                y = (-x)2 =  x2  

        so that 

                y = x2  

        is symmetric with respect to the y axis.

      2. For 

                y = x3  

                we replace with  

                y = (-x)3 = - x3  

        so that 

                y = x3  

                is not symmetric with respect to the y axis.

    3. Origin Symmetry

      To test algebraically if a graph is symmetric with respect to the origin we replace both x and y with -x and -y and see if the result is equivalent to the original expression.  

      1. For 

                y = x3

        we replace with 

                (-y) = (-x)3  

                so that 

                -y = -x3 or y = x3

        Hence  

                y = x3  

        is symmetric with respect to the origin.  

  3. Intercepts

    We define the x intercepts as the points on the graph where the graph crosses the x axis.  If a point is on the x axis, then the y coordinate of the point is 0.  Hence to find the x intercepts, we set y = 0 and solve.

    Example:  

    Find the x intercepts of

            y = x2 + x - 2

    We set y = 0 so that

            0 =  x2 + x - 2 = (x + 2)(x - 1)

    Hence that x intercepts are at (-2,0) and (1,0)

    We define the y intercepts of a graph to be the points where the graph crosses the y axis.  At these points the x coordinate is 0 hence to fine the y intercepts we set x = 0 and find y.

    Example:   

    Find the y intercepts of  

            y = x2 + x - 2

    Solution:  

    We set x = 0 to get:  

            y = 0 + 0 - 2 = -2.  

    Hence the y intercept is at (0,-2).

Back to Functions Page

Back to Math 103A Home Page

Back to the Math Department Home

e-mail Questions and Suggestions