The Ellipse
-
Definition of the Ellipse (Geometric)
Let P and Q be two points (the foci) in the plane. The ellipse is the set of all points R in the plane such that PR + QR is a fixed constant. An ellipse can be constructed using a piece of string. Fix the two ends of the string so the string is not taught. Then with a pencil pull the string so that the string is tight and move the string around to form the ellipse. Suppose that C = (h,k) is the center of the ellipse and that V is a vertex of the ellipse then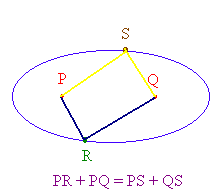
e = CP/CV
is called the eccentricity of the ellipse. This number tells us how squished the ellipse is. If the ellipse is close to being a circle e will be close to 1, while if the ellipse is very long and narrow than e will be close to 0.
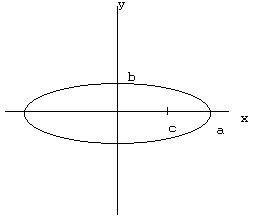
If
c = CP and a = CV
and b is the distance from the center to the vertex on the minor axis, and z is the distance from the focus to the minor axis, then by the definition of the ellipse
2z = (c + a) + (a - c) = 2a
Hence
z = a
so that
c2 = a2 + b2
If the ellipse has center (0,0) then the equation has the form
x2/a2 + y2/b2 = 1
If the center is (h,k) then the equation has the form
(x - h)2/a2 + (y - k)2/b2 = 1
Example
Find the foci and eccentricity of the ellipse
x2/9 + y2/25 = 1Solution
We have
c = (25 - 9)1/2 = 4
since b > a, the foci are on the y-axis and have coordinates
(0,-4) and (4,0)
and the eccentricity is
e = c/b = 4/5
Exercise:
Draw the ellipse with equation
9x2 + 25y2 - 36x - 4y + 103 = 0
-
Applications
Kepler's Law of Planetary Motion
Kepler's law says that any heavenly body in orbit around the sun follows the path of an ellipse with the sun as one of its foci.Exercise:
The earth orbits the sun with eccentricity .0167. The length of half the major axis is 14,957,000 km. Find the closest and farthest distance that the sun gets to the earth.The Capital Building
The ceiling of the building is in the shape of an ellipsoid. If a word is spoken from a focus, then the echo of the sound will concentrate at the other focus, hence one senator can whisper to another senator who is far away and only they can hear each other.

Back to the College Algebra Part II (Math 103B) Site
Back to the LTCC Math Department Page
e-mail Questions and Suggestions