Deductive and Inductive Reasoning

Section 1.1

Logic is the science of correct reasoning.

In problem solving, we organize information, analyze it, compare it to previous problems and come to some method for solving it.

Deductive reasoning is the process of applying a general rule or idea to a specific case.

Example1: 

Solve the equation 

        x² = 3x + 4

This equation is a quadratic equation (highest degree is 2, a squared variable).  We know that all quadratic equations can be solved using the quadratic formula (general rule). 

If  

        Ax² + Bx + C = 0        (A 0)  

then                

        x  =  

We apply the formula to our equation (specific case).

        x² – 3x –  4 = 0           

With    

        A = 1               B = -3              C = -4

        x  =  

         =     =    =  
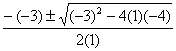
 or  

          

        x = 4     or     x = -1

A syllogism is an argument composed of two statements or premises (the major and minor premises), followed by a conclusion.  If the conclusion of the argument is guaranteed, then the argument is valid.  The argument is invalid if there is at least one instance where the conclusion does not follow. 

Example 2:  (Best known syllogism of Aristotle)

All men are mortal                             (major premise)

Socrates is a man                             (minor premise)

Therefore, Socrates is mortal          (conclusion)

Using a Venn Diagram to determine valid and invalid arguments.

You may have to draw more than one Venn Diagram for the same argument to represent all possible cases.

Do not confuse validity of an argument to the truth of the conclusion.  Truth refers to conformity with fact or experience.  Validity refers to the process of reasoning used to obtain a conclusion.

More examples in class.

Inductive Reasoning is the process of going from specific repeated cases and then applying a general rule or idea to these observations. 

Example 3: 

I drive a Subaru.

My older daughter drives a Subaru.

My younger daughter drives a Subaru.

(Specific repeated cases)

Conclusion:

Everyone in my family drives a Subaru.

(General statement)

However, the conclusion is false because my husband drives a Ford.

The conclusion in an inductive argument is never guaranteed.

Example 4:

2, 4, 6, 8,

What follows the number 8?

We see that the difference between two consecutive numbers is 2, so a probable answer would be 10.

But another possible answer is:

“Who do we appreciate?”

Deductive Reasoning:         

(General statement)  (Specific)              Conclusion is guaranteed.

Inductive Reasoning:

(Specific cases)  (General Statement)             

Conclusion may be probable, but not guaranteed.

Back to Finance, Geometry and Logic Main Page

Back to the Survey of Math Ideas Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions