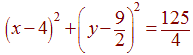Exercise
Find the equation of osculating circle to y = x2 at x = -1.
Solution
In order to find the unit tangent vector, we parameterize the curve as
r(t) = t i + t2 j
and we find
r'(t) = i + 2t j
r''(t) = 2 j
Plugging in -1 for t gives
r'(-1) = i - 2 j
r''(-1) = 2 j
||r'(-1)|| =
![]()
So that
T(-1) =
1/![]() i - 2/
i - 2/![]() j
j
We can find the principle unit normal vector by switching the coordinates of the unit tangent vector and making one of them positive. Since the principle unit normal vectors always points into the curve, we can see that it points upward from the parabola, hence both components are positive:
N(-1) =
2/![]() i - 1/
i - 1/![]() j
j
Next, we find the curvature. Since it is a plane curve, we can find the two derivatives:
f '(-1) = -2 f ''(-1) = 2
Now plug these into the curvature formula to get
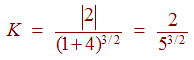
so that the radius of curvature is
![]()
and the square of this radius is
r2 = 125/4
The center of the osculating circle will be the tip of the vector:
<-1,2> + rN(-1)
Calculating, we get
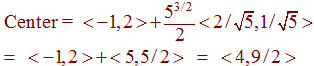
Now that we have the center and radius of the circle, we can use the standard equation for a circle to get: