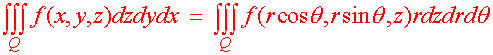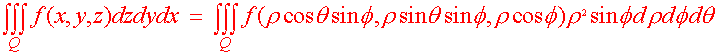Triple Integrals in Cylindrical and Spherical Coordinates
Cylindrical Coordinates
When we were working with double integrals, we saw that it was often easier to convert to polar coordinates. For triple integrals we have been introduced to three coordinate systems. The rectangular coordinate system (x,y,z) is the system that we are used to. The other two systems, cylindrical coordinates (r,q,z) and spherical coordinates (r,q,f) are the topic of this discussion.
Recall that cylindrical coordinates are most appropriate when the expression
x2 + y2
occurs. The construction is just an extension of polar coordinates.
x = r cos q y = r sin q z = z
Since triple integration can be looked at as iterated integration we have
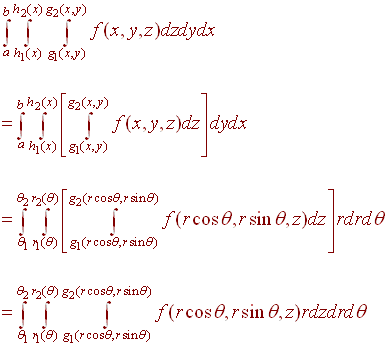
This leads us the the following theorem
|
Theorem: Integration With Cylindrical Coordinates Let f(x,y,z) be a continuous function on a solid Q. Then
|
Example
Find the moment of inertia about the z-axis of the solid that lies below the paraboloid
z = 25 - x2 - y2
inside the cylinder
x2 + y2 = 4
above the xy-plane, and has density function
r(x,y,z) = x2 + y2 + 6z
Solution
By the moment of inertia formula, we have
![]()
The region, being inside of a cylinder is ripe for cylindrical coordinates. We get
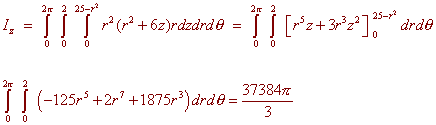
Spherical Coordinates
Another coordinate system that often comes into use is the spherical coordinate system. To review, the transformations are
x = r cosq sinf y = r sinq sinf z = r cosf
In the next section we will show that
dzdydx = r2 sinf drdfdq
This leads us to
|
Theorem: Integration With Spherical Coordinates Let f(x,y,z) be a continuous function on a solid Q. Then
|
Example
Find the volume of solid that lies inside the sphere
x2 + y2 + z2 = 2
and outside of the cone
z2 = x2 + y2
Solution
We convert to spherical coordinates. The sphere becomes
r
= ![]()
To convert the cone, we add z2 to both sides of the equation
2z2 = x2 + y2 +z2
Now convert to
2r2cos2f = r2
Canceling the r2 and solving for f we get
f
= cos-1(1/![]() ) = p/4
or 7p/4
) = p/4
or 7p/4
In spherical coordinates (since the coordinates are p periodic)
7p/4 = 3p/4
To find the volume we compute
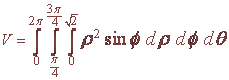
Evaluating this integral should be routine at this point and is equal to
8p
V =
3
Back to the Multiple Integration Home Page
Back to the Vector Calculus Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions