The Problem
Let
f(x) = ax2 + bx + c
If a,b, and c are chosen randomly from the interval [0,1], what is the probability that f has real roots?
The Solution
This is equivalent to finding the volume of the solid that lies inside the unit cube that lies above the discriminate surface
z2 - 4xy = 0
(Here z is b, x is a, and y is c.)
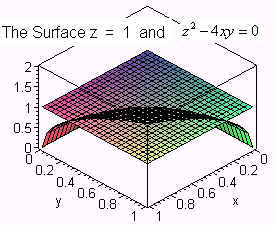
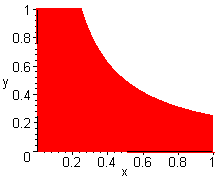
The thing to notice is that the outer limits of the triple integral is not the unit square since the surface rises above z = 1 for part of the square. This mistake will lead to the answer of 1/9. Instead it is the part of the unit square that does not lie above the curve
4xy = 1
which is shown below
We will need to break this up into two integrals as follows
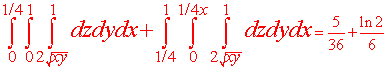
The solution is approximately equal to .25 which is significantly greater than 1/9.
Back to the Multiple Integration Page