Math 202 Practice Midterm 3
Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your work.
Problem 1 Please answer the following true or false. If false, explain why or provide a counter example. If true explain why.
A. Let f(x,y,z) be a function with continuous second order partial derivatives and let F(x,y,z) be the gradient of f(x,y,z). If S is the ellipsoid
x2
+ y2 + z2 = 1
4
oriented outward, then
![]()
False
Using the divergence theorem, we have
![]()
If gradf(x,y,z) = F, then
divF = fxx + fyy + fzz
There theorem would be true if the function was harmonic, however if it not harmonic. All bets are off. For example, if
f(x,y,z) = 1/6 (x2 + y2 + z2)
and
divF = 1/6 (2 + 2 + 2) = 1
Hence the integral represents the volume of the ellipse which is certainly not zero.
B. Let F(x,y) be a conservative vector field, then
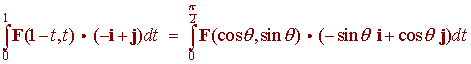
True,
The
first line integral traces out the line segment from (0,1)
to (1,0) and the second traces out the
quarter-circle from (0,1) to (1,0).
Notice that in the first integral 
r1(t) = (1 - t)i + tj r1'(t) = -i + j
and in the second integral
r2(q) = (cos q)i + (sin q)j r1'(t) = (-sin q)i +(cos q) j
By the fundamental theorem of line integral, the integral is independence of path, hence the two integrals are equal.
Problem 2
Show that
![]()
for any closed surface S.
We use Stokes' Theorem. We have
![]()
Where C is the boundary of the surface S. But since S is a closed surface, it has not boundary. Hence C is a curve of zero length and the right hand integral is zero.
Problem 3
A fish starting at the origin swims in a straight path to the point (0.2,0.1,0.3), then changes direction and swims along the circular path through the point (0.5,0.2,0.6) and the point (0.7,0.5,0.8), and finally changes directions heading straight to the point (1.5,1,2). The current can by represented by the vector field
F(x,y,z) = (2x + 2z)i + (1 - 3z)j + (2x - 3y + 5)k
Find the total work done by the current.
The important thing to not here is that
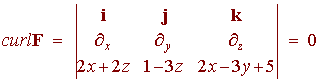
Since F is conservative, we can use the fundamental theorem of line integrals. We seek a potential function f. We have
fx = 2x + 2z
Integrating with respect to x gives
f = x2 + 2xz + C(y,z)
Now taking the derivative with respect to y gives
fy = Cy(y,z) = 1 - 3z
Integrating with respect to y gives
C(y,z) = y - 3yz + C(z)
so that
f = x2 + 2xz + y - 3yz + C(z)
Now we take the derivative with respect to z to get
2z - 3y + C'(z) = 2x - 3y + 5
so that
C'(z) = 5
Integrate with respect to z to get
C(z) = 5z
Hence
f(x,y,z) = x2 + 2xz + y - 3yz + 5z
The fundamental theorem of line integrals gives that the integral is
f(1.5,1,2) - f(0.2,0.1,0.3) =
[(1.5)2 + 2(1.5)(2) + 1 - 3(1)(2) + 5(2)] - [(0.2)2 + 2(0.2)(0.3) + 0.1 - 3(0.1)(0.3) + 5(0.3)]
= 11.58
Problem 4
Evaluate
![]() where F
is the vector field
where F
is the vector field
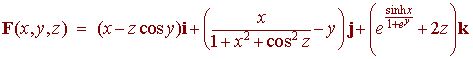
and S is the rectangular solid with vertices (0,0,0), (1,0,0), (1,2,0), (0,2,0), (0,0,3), (1,0,3), (1,2,3), (0,2,3).
We use the divergence theorem. We have
divF = 1 - 1 + 2 = 2
We have
![]()
Since the integrand of the right hand side is just a constant, its value is equal to the constant times the volume of the solid. Since the solid is a rectangular solid with side lengths 1, 2, and 3, we have
2(Volume E) = 2(1)(2)(3) = 12
Problem 5
Find the work done by sailing a ship from the point (2,3) the the point (-1,2) against the wind with velocity field
F(x,y) = yi + (3x + 2y)j
First notice that F is not a conservative vector field. We need to parameterize the curve and perform the line integral. The curve can be parameterized by
r(t) = (2 + (-1 - 2)t)i + (3 + (2 - 3))j = (2 - 3t)i + (3 - t)j
We have
dr = -3i - j
F(t) = (3 - t)i + (3(2 - 3t) + 2(3 - t))j = (3 - t)i + (12 - 11t)j
The integrand becomes
F . dr = -3(3 - t) + (-1)(12 - 11t) = -21 + 14t
Now we integrate
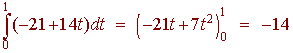
Problem 6
Find the flux of F through the surface S where
F(x,y,z) = 3zi - 4j + yk
and S is the part of the plane
x + y + z = 1
in the first octant with upwardly pointing unit normal.
We use Stokes' theorem. We have
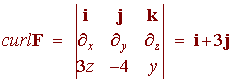
We can write the surface as
z = 1 - x - y
Using Stokes theorem we get
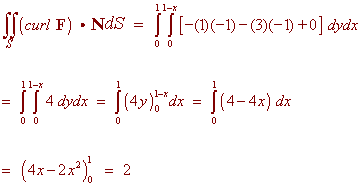
Let F and G be differentiable transformations from R2 to R2 such that for both of these transformations x(u,v) = f (u) is a function of only u and y(u,v) = g(v) is a function of only v. Prove that
JFoG = JGoF
Solution
Let
F: x(u,v) = a(u), y(u,v) = b(v)
G: x(s,t) = c(s), y(s,t) = d(t)
Then since
JFoG = JF JG
Notice that half of the partial derivatives are zero. We have
![J_F = Matrix[(a_u,0),(0,b_v)], J_G = Matrix[(c_s,0),(0,d_t)]](imgC.gif)
Now, use the multiplication rule for Jacobians to get
![JFoG = JFJG = Matrix[(au,0),(0,bv)]Matrix[(cs,0),(0,dt)]=Matrix[(cs,0),(0,dt)]Matrix[(au,0),(0,bv)]=JGJF = JGoF](imgF.gif)