MATH 202 PRACTICE MIDTERM 2

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

PROBLEM 1  Please answer the following true or false.  If false, explain why or provide a counter example.  If true explain why. 

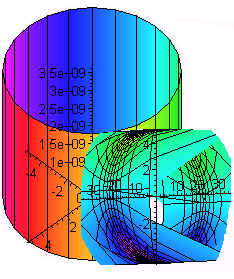
A)   If all six limits of integration of an integral written in spherical coordinates are constants, then the region of integration is a sphere.

Solution

False, it can be a part of a sphere.  For example

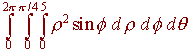
represents a cone with a rounded top.

B)   

Solution

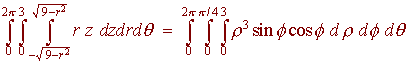
False,  the integrands work out when you convert, but the regions are different.  The left side is the part of the sphere of radius 9 inside the cylinder of radius 3 and the right side is a cone.

PROBLEM 2 Set up integrals to evaluate the following.  Use the coordinate system that will most effectively solve the integral. 

A.     The mass of the tetrahedron that lies in the first octant and below the plane x + y + 2z  =  2  such that the density function is f(x,y,z)  =  3yz .

  Solution

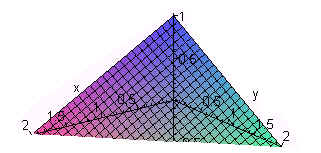
The tetrahedron is pictured below.  We find the triple integral (using dzdydx)  The bottom is z  =  0 and the top is 

z  =  2 - .5(x + y)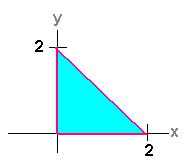

To find the outer limits we draw the projection of the surface on the xy-plane as shown to the right.  The bottom curve is y  =  0 and the top curve is  y  =  -x + 2.  The farthest to the left that x gets is 0 and the farthest to the right is 2.  Putting this together, we get

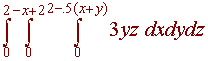
B.     The surface area of the part of the paraboloid  z  =  9 - x² - y²   that lies above the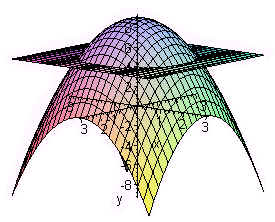 plane z = 5 .  

Solution

The picture is shown to the right. We can use polar coordinates to simplify the region which is a circle of radius 2 since solving 

        9 - r²  =  5 

gives r  =  2.

 The paraboloid becomes.  We have 

        z_x  =  -2x        z_y  =  -2y

so that

        1 + z_x² + z_y²  =  1 + 4x² + 4y²  =  1 + 4r² 

Putting this all together gives

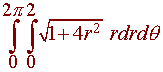
C.     The moment of inertia about the z-axis of the solid between the cylinders  x² + y²  =  25  and  x² + z²  =  25 that has density function 1.  

Solution

  Changing to polar coordinates gives

        r  =  5        and      r²cos² q + z²  =  25

the inner limits are 

The outer limits just come from the circle of radius 5.  The integrand is 

        x² + y²  =  r² r  =  r³ 

Putting this together gives

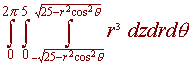
PROBLEM 3

Switch the order of integration.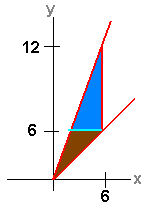 

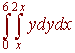
Solution

The key to this problem is to graph the region and notice that to integrate with dxdy we must break the region into two pieces.  As shown to the right.  We get

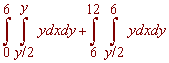
PROBLEM 4

A master dart thrower has determined that her probability density function is inversely proportional to one more than the fourth power of the distance in centimeters from the center of the dartboard. 

Find the constant of proportionality.  (Hint:    )  

Solution

We integrate

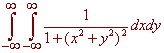
by transforming to polar coordinates.  We get

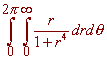
To integrate this we can use u-substitution with

        u  =  r²      du  =  2r dr

This gives

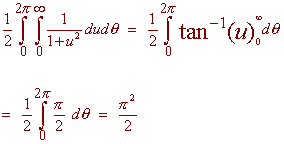
Since the probability must be equal to one, the constant of proportionality must be the reciprocal of this double integral that is

                    2
        k  =                    
                    p²

  Solution

We work the same problem except that the region of integration is the circle of radius 1 and we include the constant of proportionality.  We have

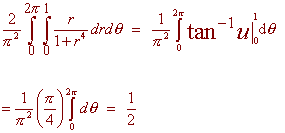
PROBLEM 5

Consider the solid described by

        (x + 2y)² + (2y - 2z)² + (x + z)²  < 25    

with density function 

        f(x,y)  =  x + 2y                 

Show that the mass of the solid is equal to 

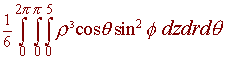
Hint:  Recall that  

Solution

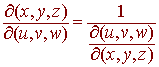
We use Jacobians with 

        u  =  x + 2y        v  =  2y+2z        w  =  x + z

We have

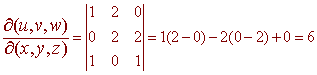
Thus the Jacobian is 1/6.  The function f becomes u.  The region becomes 

        u² + v² + w²  < 25 

which is a sphere of radius 5.  The result follows when we put this region in spherical coordinates (using (u,v,w) instead of (x,y,z)).