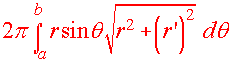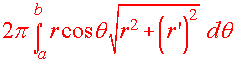Polar Area and Acrlength
Area
If we have a region defined by
r = r(q),
q = a and
q = b
what
is the area of the region? If r is the arc of a circle then we want to find the area of the sector of
the circle. If
q
= b - a 
then the area
A = 1/2 q r2
This is true since the area of the entire circle is p
r2. We
can set up the relationship:
A
q
=
p
r2
2p
so that
p r2 q
1
A =
= q
r2
2p
2
Cutting the region into tiny dq pieces, we have
1
A =
r2(q)dq
2
Adding up all the pieces, we arrive at
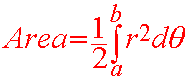
|
Exercise
Find the area enclosed by the curve
r = 2 cos q
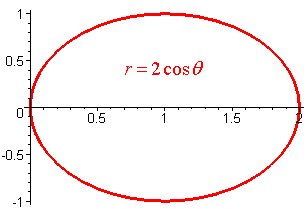
Arclength
Since the arclength of a parameterized curve is given by
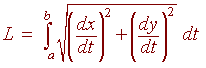
we have that for polar coordinates, letting
x(q) = r(q)
cos q = r cos q
and
y(q) = r(q)
sin q = r sin q
we have
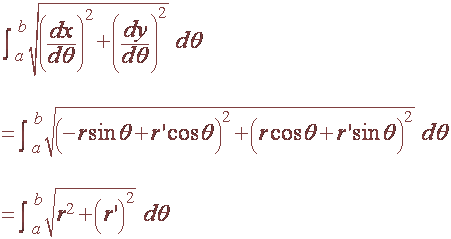
We also have that the surface area of revolution is
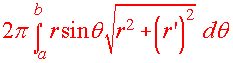
Example
Find the length of the 8 petalled flower 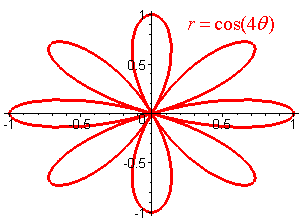
r = cos(4q)
Solution
We find the length of one of the petals and multiply by 8. We see that the right petal goes through the origin at
-p/8 and next at p/8.
Hence we integrate
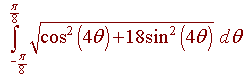
This is best done with a calculator which gives an answer of 2.26.
Exercise
Find the length of the curve
r = 5(1 + cos(q))
between 0 and 2p.
Surface Area of Revolution
We have the following two formulas: If r = r(q) is revolved around the polar axis
(x-axis) then the Surface
area is
| Surface Area (Revolved Around the x-axis)
|
If it is revolved around the y-axis then the resulting surface area is
| Surface Area (Revolved Around the y-axis)
|
Example:
Use your graphing calculator to find the area that
results when
r
= 1 + cosq
is revolved around the y-axis.
Solution
We have
r' =
-sin q
Putting this into the formula gives
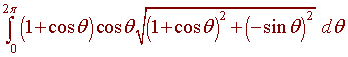
The Calculator gives and answer of 6.4.
Back to the Polar and Parametric Equations Page
Back to the Math 107 Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions