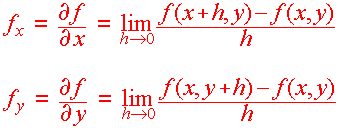Partial Derivatives
Definition of a Partial Derivative
Let f(x,y) be a function of two variables. Then we define the partial
derivatives as
|
Definition of the Partial Derivative
|
if these limits exist.
Algebraically, we can think of the partial derivative of a function with
respect to x as the derivative of the function with
y held constant.
Geometrically, the derivative with respect to x at a point
P represents
the slope of the curve that passes through P whose projection onto the
xy
plane is a horizontal line. (If you travel due East, how steep are
you climbing?)
Example
Let
f(x,y) = 2x + 3y
then
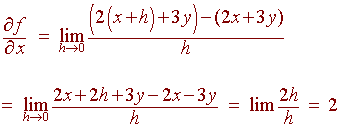
We also use the notation fx
and fy
for the partial derivatives with respect to x and y respectively.
Exercise:
Find fy for the function from the example above.
Finding Partial Derivatives the Easy Way
Since a partial derivative with respect to x is a derivative with the rest of the variables held constant, we can find the partial derivative by taking the regular derivative considering the rest of the variables as constants.
Example
Let
f(x,y) = 3xy2 -
2x2y
then
fx = 3y2 - 4xy
and
fy
= 6xy - 2x2
Exercises
Find both partial derivatives for
-
f(x,y) = xy sin x
-
x + y
f(x,y) =
x - y
Higher Order Partials
Just as with function of one variable, we can define second derivatives for
functions of two variables. For
functions of two variables, we have four types:
fxx,
fxy fyx
and fyy
Example
Let
f(x,y) = y ex
then
fx =
yex
and
fy = ex
Now taking the partials of each of these we get:
fxx =
y ex
fxy = ex fyx = ex
and fyy = 0
Notice that
fxy = fyx
|
Theorem |
Functions of More Than Two Variables
Suppose that
f(x,y,z) = xy - 2yz
is a function of three variables,
then we can define the partial derivatives in much the same way as we defined
the partial derivatives for three variables.
We have
fx = y
fy = x - 2z
and fz = -2y
Application: The Heat Equation
Suppose that a building has a door open during a snowy day. It can
be shown that the equation
Ht = c2Hxx
models this situation where H is the heat of the room at the point
x feet
away from the door at time t. Show that
H = e-t cos(x/c)
satisfies this differential equation.
Solution
We have
Ht
= -e-t cos(x/c)
Hx = -1/c e-t
sin(x/c)
Hxx = -1/c2 e-t
cos(x/c)
So that
c2Hxx =
-e-t cos(x/c)
And the result follows.
Back to the Functions of Several Variables Page
Back to the Math 107 Home Page