Functions of Several Variables
Definition of Functions of Several Variables
A function of several variables is a function where the domain is a subset
of Rn and range is
R.
Example:
f(x,y) = x - y
is a function of two variables
x - y
g(x,y,z) =
y - z
is a function of three variables.
Finding the Domain
To find the domain of a function of several variables, we look for zero
denominators and negatives under square roots:
Example
Find the domain of
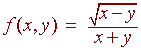
First, the inside of the square root must be positive, that is
x - y > 0
second, the denominator must be nonzero, that is
x + y
![]() 0
0
hence we need to stay off the line 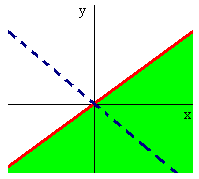
y = -x
Putting this together gives
{(x,y) | x - y > 0 and
y ![]() -x}
-x}
The graph to the right shows the domain as the shaded green region.
.
Exercise
Find the domain of the function
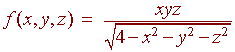
Level Curves
The topographical map shown below is of the Rubicon Trail. It represents the function that maps a longitude and latitude to an altitude.
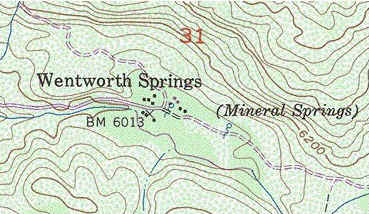
Each curve represents a path where the z-coordinate (altitude) is a constant. Crossing many topo lines in a short distance represents a path that is very steep.
Now lets make our own contour map of the function.
f(x,y) = y - x2
by setting constant values
for z:
| z | Equation |
| 1 | y = x2 + 1 |
| 2 | y = x2 + 2 |
We see that each topo line is a parabola and that the y-intercept gives the height. Below is a contour diagram of this function.
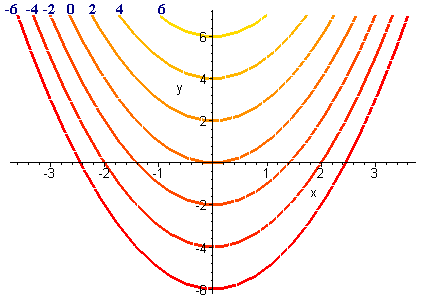
Names for the curves drawn are level curves, isotherms (for temperature), isobars (for pressure), and equipotential lines (for electric potential fields) depending on what the two variable function represents.
Back to the Functions of Several Variables Page
Back to the Math 107 Home Page