Hyperbolic Functions

I.  Quiz

II.  Homework Questions

III.  Definition of the Hyperbolic Functions

We define the hyperbolic functions as follows:

1. sinh(x) = [e^x - e^-x]/2

2. cosh(x) = [e^x + e^-x]/2 

3. tanh(x) = sinh(x)/cosh(x)

We will show that

1. (cosh(x))² - (sinh(x))² = 1 

2. d/dx(sinh(x)) = cosh(x)

3. d/dx(cosh(x)) = sinh(x)

Theorem:

1. d/dx sinh^-1(x) = 1/sqrt(1 + x²)

2. d/dx cosh^-1(x) = 1/sqrt(x²  - 1)

3. d/dx tanh^-1(x) = d/dx coth^-1(x) = 1/(1 - x²)

4. d/dx sech^-1(x) = 1/xsqrt(1 - x²)

5. d/dx csch^-1(x) = 1/xsqrt(1 + x²)

Example:  

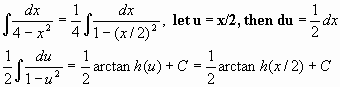
VI.  The derivative of the inverse hyperbolic trig functions

Example:  Find the derivative of arctanhx

Taking derivatives implicitly, we have

[arctanh(x)]' = 1/sech²(arctanh(x))

Since cosh²(x) - sinh²(x) = 1, dividing by cosh²(x), we get

1 - tanh²(x) = sech²(x)

so that

[arctanh(x)]' = 1/sech²(arctanh(x)) = 1/[1 - tanh²(arctanh(x))] = 1/[1 - x²]