Logs and Derivatives
Definition of the Natural Logarithm
Recall that
![]()
What is
![]()
Definition: For x > 0 we define
|
|
Note: The Second Fundamental Theorem of Calculus tells us that
d/dx
(ln x) = 1/x
Properties of ln x
-
ln 1 = 0
-
ln(ab) = ln a + ln b
-
ln(an) = n ln a
-
ln(a/b) = ln a - ln b
Proof of (3)
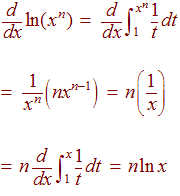
So that
ln(xn)
and
n ln x
have the same derivative. Hence
ln(xn) =
n ln x + C
Plugging in x = 1 we have that C =
0.
Definition of e
Let e be such that
ln e = 1
ie.
|
|
Examples and Exercises
Example
Find the derivative of
ln (x2 + 1)
Solution
We use the chain rule with
y = ln u,
u = x2 + 1
2x
y' = (2x)(1/u)
=
x2 + 1
Find the derivatives of the following functions:
-
ln (lnx)

-
(ln x)/x

-
(ln x)2

ln (sec x)

ln (csc x)

-
Show that
3 ln x - 4
is a solution of the differential equationxy'' + y' = 0
Find the relative extrema of
x ln x
Find the equation of the tangent line to
y = 3x2 - ln x
at (1,3)
Find dy/dx for
ln(xy) + 2x2 = 30
Back to the Math Department Home
e-mail Questions and Suggestions