The Volume of Cored Sphere
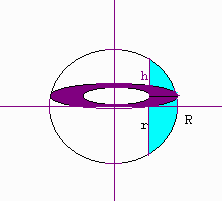
Let S be a sphere of radius R, center at the origin and let C be a cylinder of radius r (r < R) with the z-axis the axis of rotation. We are concerned with the volume of the part of S outside C. This cored sphere can also be realized by taking the region bounded by the circle
x2 + y2 = R2
and the line
x = r
and revolving it around the y-axis. Taking a cross-section perpendicular
to the y-axis and revolving it around the y-axis produces a washer. The
inner radius of the washer is r and the square of the outer radius of the washer
is
R2 - y2
Let h be the the height of the region
(from the x-axis).
h = R2 - r2
Hence the area of the washer is
Area = p[(R2 - y2 ) - r2] = p[(R2 - r2 ) - y2] = p[h2 - y2]
The smallest y value the cross-section will have is -h and the largest is h.
We can write this as an integral
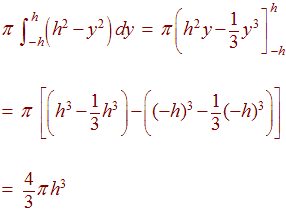
Notice that the volume only depends on the height of the region.