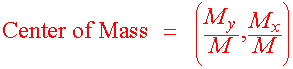Moments and Centroids
Mass and Slugs
Newton's Law states that
|
F = ma |
where F is the force, m is the mass, and
a is the acceleration. In
the US system, Force is measured in pounds and mass is measures in slugs.
Example:
I weigh 165 lbs. What is my mass?
Solution:
Since weight corresponds with gravitational force, and the acceleration of
gravity is 32 ft/sec2 we have
165 = 32m
or
m = 5.15 slugs.
In the metric system, kg is a mass unit and Newtons is a weight unit.
Moments and Center of Mass for Discrete Mass Points
Suppose that we have a teeter totter and a 10 kg child is on the left 5 meters from the center of the teeter totter and a 15 kg child is on the right 4 meters from the center of the teeter totter. We define the moment as:
10(-5) + 15(4) = 10
In general, we define the moment for masses mi at the points xi to be
Moment = S mi xi
If the moment is 0 then we say that the system is in equilibrium.
Otherwise, let x
be the value such that
S
mi
(xi - x) = 0
Then
x is called the center of mass
of the system.
|
Theorem x = moment/total mass |
Proof:
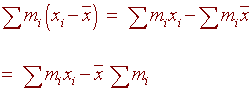
so that
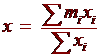
Example:
Find the center of mass of the teeter totter.
Solution
We have
moment = 10
and
total mass = 25
hence the
center of mass = 10/25 = 0.4
We can say that if the center of the teeter totter was 0.4 meters from the current center, then the children would be in balance.
For points in the plane, we can find moments and centers of mass coordinate wise.
We define:
mx = moment about the x axis = S mi
xi |
Example:
For the points (-3,0) with mass 4,
(2,2) with mass 3, and
(1,-2) with mass 1 we have
mx = (4)(-3) + (3)(2) + (1)(1) = -5
my = (4)(0) + (3)(2) + (1)(-2) = 8
Center of Mass = (-5/8,8/8) =
(-0.625,1)
Center of Mass for a Two Dimensional Plate
First, we recall that for a region of density r bounded by f(x) and g(x)
|
Mass =
(Density)(Area) =
Mx =
My =
|
and
|
|
Example
Find the center of mass for the plate of constant density
2 that is bounded by the curves
y = 1 - x,
y = 0 and x = 0
We have
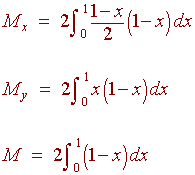
Pappus Theorem
Suppose that we revolve a region around the y-axis. Then the volume of revolution is:
V = 2prA
where A is the area of the region and r is the distance from
the centroid (constant density) to the axis of rotation.
Example
Suppose that we revolve the 4 x 4 frame with width 1 centered about (6,2) about the y-axis. Then we have that the Area is
A = 4 + 4 + 2 + 2 = 12
R = 7
so that
V = 2p7(12) = 168p
Exercise
Find the volume of the torus formed by revolving the
disk
(x - 11)2 + y2 = 4
about the y-axis.
Back to the Math Department Home
e-mail Questions and Suggestions