MATH 105 PRACTICE MIDTERM III KEY

 

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

 

 

PROBLEM 1  Please answer the following true or false.  If false, explain why or provide a counter example.  If true, explain why.

 

A)   If f(x) is a positive continuous function such that

         

 then

           

cannot be equal to 3.

Solution

        True, since f is a positive function, both integrals represent areas,  and the second integral represents an area of a region that contains the region of the first integral.  Hence the second integral must be at least as large as 4.

       

 

 

 

 

 

 

 

 

 

 

B) If f(x)  is a differentiable function such that the equation of the tangent line at 

        x = 2

 is

                   1           1
        y  =         x  -                     
                   2           2

and if x = 2 is the first guess in Newton’s method, then x = 1  is the second guess.

Solution

        True,  We arrive at the second guess by finding the x-intercept of the tangent line.  Since the x-intercept is 1, x  =  1 is the second guess.  

 

       

 

 

 

 

 

 

 

 

 

C)   If f(x) and g(x) are continuous functions on [a,b], then          

        

Solution

        False, for example, if f(x)  =  g(x)  =  1 and if a  =  0 and b  =  2, then the left hand side is 2 and the right hand side is (2)(2)  =  4

 

 

       

 

 

 

 

 

 

 

 

 

PROBLEM 2 Evaluate the following integrals:

A.        

Solution

        Just integrate the terms individually:

        -cos x  -  2/3 x3/2 + 2/3 x3  -  3x  + C

       

 

 

 

 

 

 

 

 

 

B.        

        Solution

                We use u-substitution:

                u  =  1 - x        du  =  -1dx    dx  =  -du    x  =  1 - u

                when 

                    x  =  2    u  =  -1

                when 

                    x  =  3    u  =  -2

            Substituting produces

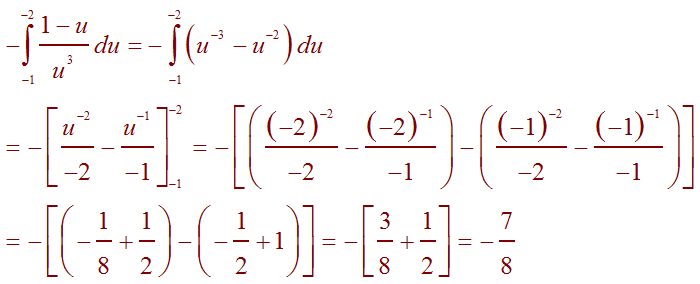
            Integration using substitution

 

       

 

 

 

 

 

 

 

 

 

 

C.        

    Solution

                We use u-substitution:

                u  =  2x        du  =  2dx        dx  =  1/2 du

                Substituting, we get

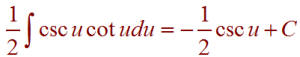
                1/2 int(cscu cotu du) = -1/2 cscu + C

                Resubstituting, gives

               -1/2csc(2x) + C

 

 

 

       

 

 

 

 

 

 

 

 

 

 

PROBLEM 3 Use Riemann Sums to find the area of the region below the curve y = 9 - x2, above the x-axis, and between x = 1 and x = 3.

  Solution

            We have 

                    Dx  =  (3 - 1) / n  =  2/n

              Hence

               

       

 

 

 

 

 

 

 

 

 

 

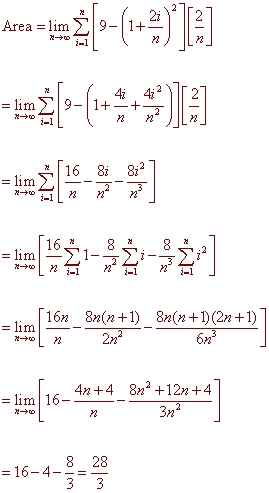
PROBLEM 4 

Let  

         

Find  F'(x)  

     Solution

          Use the chain rule along with the second fundamental theorem of calculus:

        u  =  sin x       

        u'(x)  =  cos x       

         F'(u)  =  cos u2  =  cos(sin2 x)        By the fundamental theorem of calculus

        Now use the chain rule

        F'(x)  =  u'(x)F'(u)  =  (cos x)(cos(sin2 x))

 

       

 

 

 

 

 

 

 

 

 

PROBLEM 5

You are the owner of Tahoe Winter Wear and need to determine the best price to sell your most popular winter jacket.  Your cost for selling the jackets is

C = 50 + 20x

Where x is the amount to jackets that you sell.  Your research shows that the relationship between price, p, and the number of jackets that you can sell, x, is
                        p = 300 – 10x
How much should you charge for your jacket in order to maximize profit?

  Solution

        First calculate the revenue R:

            R  =  xp  =  x(300 - 10x)  =  300x - 10x2

        Now use the fact that Profit equals Revenue minus Cost:

        P  =  R - C  =  (300x - 10x2) - (50 + 20x)  =  280x - 10x2 - 50

        To find the maximum profit we take the derivative and set it equal to zero:

        P'  =  280 - 20x = 0

        x  =  14

        Now substitute 14 for x in the demand equation:

        p  =  300 - 10(14)  =  160

        You should charge $160 for the jacket.

 

       

 

 

 

 

 

 

 

 

 

PROBLEM 6  

You are manufacturing a square computer chip.  Your machine can construct the square with side length 0.4 0.0002  cm.  Use differentials to approximate the maximum percent error in the area of the chip.

      Solution

                Use the formula

                        A  =  x2

                        A'  =  2x

                Differentials gives

                        DA  @  2xDx  =  2(0.4)(0.0002)  =  0.00016

                To find the percent error, use

                        Percent Error  =  (DA/A)(100%)  =  (0.00016/.42)(100%)  =  0.1%

 

       

 

 

 

 

 

 

 

 

 

 PROBLEM 7

 

Let f(x)  =  x3 + x + 4

  1. Prove that f(x) has an inverse function.

    Solution

     We use the theorem that tell us that if f(x) is monotonic then the inverse exists.  We have 

            f '(x)  =  3x2 + 1

    Which is always positive, hence f(x) is monotonically increasing.  Therefore f has an inverse.

     

     

     

     

     

     

     

     

     

     

     

     

  2. Let g(x)  be the inverse of f(x).  Find g'(4) .

    Solution

    We use the formula 

                                1
            g '(4)  =                      
                              f '(g(4))

    We find g(4) by setting f(x) equal to 4:

            4  =  x3 + x + 4

            x3 + x  =  0            x(x2 + 1)  =  0

    Hence x  =  0.  Now calculate

            f '(0)  =  3(0)2 + 1  =  1

    Finally

                            1
            g '(4)  =           =  1
                             1

 

 

 

 

 

 

 

 

 

Back to Math 105 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions