Name                                    

MATH 105 PRACTICE MIDTERM 1 KEY

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

PROBLEM 1  Please answer the following true or false.  If false, explain why or provide a counter example.  If true, explain why.

A)     (7 Points)  If f(x)  and g(x)  are differentiable functions with

           f '(5)  =  10    and    g'(5)  =  4

then if

                           f(x)
     h(x)   =           -  3g(x)
                      2 

        then

            h'(5) = -7

  Solution:  

True:  

        h'(x) = (f(x)/2 - 3g(x))' 

        = f '(x)/2 - 3g '(x)

So that 

        h'(5) = f '(5)/2 - 3g '(5) = 10/2 - 3(4) = -7

B)     (7 Points)  Let f(x)  and g(x)  be continuous functions
     f(1)  >  g(1)       and      f(2) < g(2)
then if
     h(x) = f(x) - g(x)
h(x)  has a root for some value of x between 1 and 2.

Solution:

        True:

                    h(1) =  f(1) - g(1) > 0

                    h(2) =  f(2) - g(2) < 0

        Hence by the Intermediate Value Theorem, there is a c with h(c) = 0.

C)     (7 Points)  Let f(x)  and g(x)  be continuous functions such that

    and    

            Then h(x) has a vertical asymptote at x = 2.

                Solution:

                    False, Let f(x) = x - 2        and g(x) = x - 2

PROBLEM 2 Find the following limits if they exist:

A) (8 Points)  

     Solution   

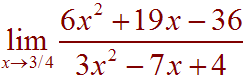
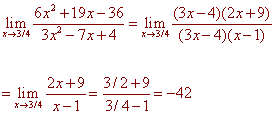
B) (8 Points)   

Solution

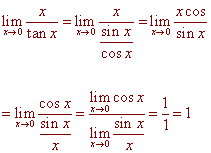
C)    (8 Points) 

          Solution

PROBLEM 3

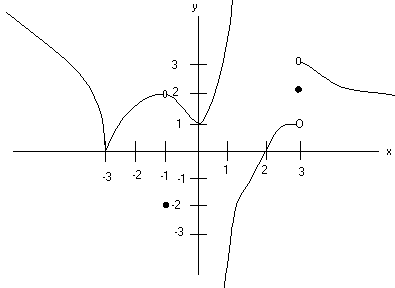
A)   (8 Points)  Find the following limits if they exist

                   i)     ii)      iii)      iv)      v)  

Solution:

        i)  0    ii)  2    iii)  1    iv)  Does Not Exist    v)  Does Not Exist

B)    (8 Points)  At which values is f(x) not continuous?

        Solution:

                -1, 1, and 3

C)   (8 Points)  At which values is f(x) not differentiable?  

        Solution:

                -3, -1, 1, and 3

PROBLEM 4   (20 Points)  Below is the function y = f(x).  Sketch a graph of the derivative y = f ’(x).

Solution

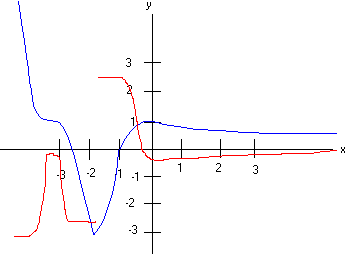
PROBLEM 5   Find f ' (x) for the following

A)    (10 Points)   

    Solution:

B)     (11 Points)   

        Solution:

            -10x^-6 - 2x + 2cosx - 2xsinx + 2cosxsinx + 5/2 x^3/2

PROBLEM 6 Let

A)    (10 Points)  Use the limit definition of the derivative to find f ’(x).

        Solution:

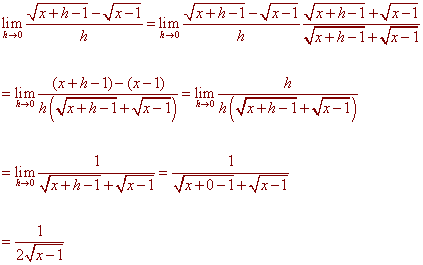
B)     (10 Points)  Prove using the e-d  definition of the limit that  

        Solution:

                Let e > 0 , choose d = e/2.

                  Then  

                        |x - 2| < d

                   implies that 

                        |x - 2| < e/2

                    so that

                        |2x - 4| < e

                    or

                        |4 - 2x| < e

                    adding and subtracting two gives 

                        |4 + 2 - 2x - 2| < e

                        |6 - 2x - 2| < e

                   Hence

                        |f(x) - 2| < e

                     So that that the limit exists.   

PROBLEM 7 (20 Points)

The position of a robin flying through the wind is given by

           s(t)  =  -5t + tcost

Find its acceleration when t is 2 seconds.

          Solution:  

                The acceleration is just the second derivative, so first compute the first derivative.

                    s '(t) = -5 + cost - tsint

            Now the second derivative is the derivative of the derivative:

                    s ''(t) = (s'(t))' = -sint - sint - tcost = -2sint - tcost

            Finally, plug in t = 2 to get

                    s ''(2) = -2sin2 - 2cos2 

            which is approximately  -1.