A Difficult Calculus Problem
Let
![]()
and let g(x) be an antiderivative of f(x). Then if
g(5) = 7
find
g(1)
Solution
Since g(x) is an antiderivative of f(x), we have
g '(x) = f(x)
or
![]()
None of the regular techniques of integration will work on this integral. Even the computer cannot solve this explicitly. Instead of integrating, we let
h(x) = g(x) - 7
Then h(x) is also an antiderivative of f(x) and
h(5) = 0
We can write
![]()
Notice that when we plug in 5 for x, we get 0 as required, since the upper and lower limits are equal. Now use a calculator to easily find
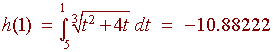
finally since
h(x) = g(x) - 7
it follows that
g(x) = h(x) + 7
and that
g(1) = h(1) + 7 = -10.88222 + 7 = -3.88222