Continuity
Continuity
If a graph has no holes asymptotes, or breaks then the
function is continuous. Or if you can draw the function without lifting
your pencil then it is continuous. Below is a formal definition.
|
Definition of Continuity
|
Note that in order for a function to be continuous at a point, three things must
be true:
-
The limit must exist at that point.
-
The function must be defined at that point, and
-
The limit and the function must have equal values at that point.
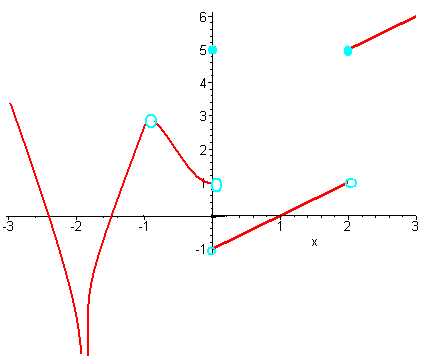
Notice that the function represented by the graph above is not continuous
at
x = -2, x = -1,
x = 0, and x = 2
Below is a list of function that are continuous.
Continuous Functions:
-
Polynomials
-
sin and cos
-
Rational Functions where the denominator is nonzero
-
Sums, Differences, and Products of continuous functions
-
Quotients of continuous functions where the denominator function is nonzero
-
Compositions of continuous functions
Examples:
The following are continuous:
-
y = x2 + 3x - 4
-
y = x sin x
-
1
y =
1+ x2
Exercises:
Determine whether the following are continuous. If
they are not continuous, at which points are they discontinuous?
-
x - 1
y =
x + 1
-
x
y =
x2 + 3x - 4
-
y = { 2x + 3 for x < 1 3x - 2 for x > 1 -
y = { x2 for x < 2 5x - 6 for x > 2
-
For what value of k is the function continuous?
f(x) = { 3x2 -5 for x < 1 5x + k for x > 1
For a function with a break the limit does not exist, however it is still interesting to consider where the path is heading towards on the left side and where it heading on the right. For example if
|x|
f(x)
=
x
then for x negative
f(x) =
-1
while for x positive,
f(x) = 1
We write
![]()
and
![]()
The Intermediate Value Theorem
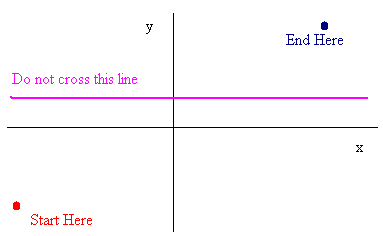
Suppose a continuous function starts at the bottom left of
the xy-plane and ends at the top right of the xy-plane. Now draw a
horizontal line somewhere in the middle of the page. Can you draw a
continuous function (that is without lifting the pencil from the paper) from
the bottom left to the top right without crossing the line? The answer
is certainly no. Try it! The intermediate value theorem
formalizes this idea.
|
The Intermediate Value Theorem
If f is continuous on [a,b] and f(a) < k < f(b) then there exists
at least one number c in the closed interval
[a,b] for which |
In particular if f(a) and f(b)
have different signs, then f has a root between
a and b.
Example
Show that the curve defined by
y =
8x7 + x4 - 2x3 + x - 3
has a root between -1 and 1.
Solution
We apply the intermediate value theorem. The
function
f(x)
= 8x7 + x4 - 2x3 + x - 3
is continuous between -1 and 1, since it is a polynomial. We
have
f(-1) = -8
+ 1 + 2 - 1 - 3 = -9
and
f(1) = 8 +
1 - 2 + 1 - 3 = 5
Since
f(-1) <
0 < f(1) Here
k = 0
By the Intermediate Value Theorem, there is a c between
-1 and 1
with
f(c) = 0
Exercise:
Write psudocode to find a root of a function
Weisstein's World of Mathematics