Newton's Method
Newton's Method
Consider finding the root of
y
= ex - 4x
Try as you may, there is no algebraic technique that finds this root.
We will approximate the solution as follows:
The graph shows that a solution lies between 0 and 2.
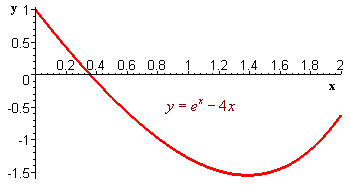
Our initial guess is
x
= 1
Now draw a tangent line through (1,f(1)). Next
see where the tangent line crosses the x-axis. The tangent line is a close
approximation to the curve for nearby values, hence the x-intercept of the
tangent line is close to the x-intercept of the curve. The tangent line
has equation
y - f(1) = f '(1)(x - 1)
The x intercept occurs when y = 0, hence
-f(1)
= f '(1)(x - 1)
solving for x,
f(1)
x
= 1 -
f '(1)
This x will not be the true root, but will
be a better guess than x = 1. We will use
this (call it x2) as our
second guess. Next play the same game:
f(x2)
x3
= x2 -
f '(x2)
The graph below shows this construction. The blue line is the first tangent line and the purple line is the second tangent line.
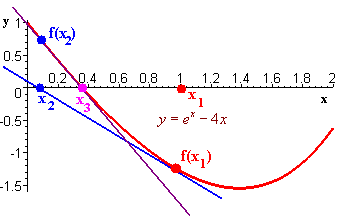
Continue this process to get
|
f(xn) |
For our example this expression is
![]()
Use a calculator or computer to find the values.
x1 = 1, x2 = 0,
x3 =.3333, x4 = .3572,
x5 =.3574, x6 = .3574
We see that .3574 is the root accurate to 4
decimal places.
Exercise
Estimate
![]()
using Newton's method.
Hint: Find the root of x2 - 5.
When Newton's Method Fails
-
If our first guess (or any guesses thereafter) is a point at which there is a horizontal tangent line, then this line will never hit the x-axis, and Newton's Method will fail to locate a root. If there is a horizontal tangent line then the derivative is zero, and we cannot divide by f '(x) as the formula requires.
-
If our guesses oscillate back and forth then Newton's method will not work.
-
If there are two roots, we must have a first guess near the root that we are interested in, otherwise Newton's method will find the wrong root.
-
If there are no roots, then Newton's method will fail to find it. (This can be frustrating when you are using your calculator to find a root.
Example
Explain why Newton's method fails to find the root of
f(x) = x1/3
with an initial guess of x = 1.
Solution
We have
f '(x) = 1/3 x -2/3
so that
xn1/3
xn+1 = xn -
= xn - 3xn = -2xn
1/3 x -2/3
This gives us
x1 = 1, x2 = -2(1) = -2
x3 = -2(-2) = 4, x4 = -2(4) = -8
These numbers are growing (in absolute value) instead of converging. In fact, we have
xn = (-1)n 2n-1
Hence Newton's method fails. However, it is clear that there is a root at x = 0. Notice that at x = 0, the derivative is undefined.
An app to explore Newton's Method
A proof that Newton's Method will always converge for a cubic with a positive derivative.