The Pythagorean Theorem
In this lesson, we will learn what the Pythagorean Theorem is and how to use it to find a missing side of a right triangle.
Thousands of years ago a Greek organization called the Pythagoreans, led by a man named Pythagoras, explored geometry. Their most important achievement involved the discovery of the relationship between the side lengths of a right triangle. This relationship, called the Pythagorean Theorem, is considered the most important formula in mathematics.
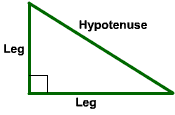
First we will recall some terminology. Recall that a right triangle is a triangle where one of its angles is 90 degrees. For a right triangle, the side that is opposite of the right angle is called the hypotenuse. This side will always be the longest side of the right triangle. The other two (shorter) sides are called legs.
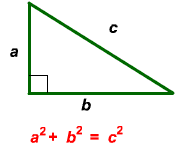
The Pythagorean Theorem states that if you add the squares of the lengths of the two legs of a right triangle you will always obtain the square of the length of the hypotenuse.
|
Example 1
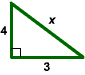
Consider the right triangle shown below. Find the value of x.
Solution
First notice that the lengths of the two legs are 4 and 3. The length of the hypotenuse is x. Using the letters from the Pythagorean Theorem, we have
a = 4
b = 3
c = x
Now we use the Pythagorean Theorem
a2 + b2 = c2
or
42 + 32 = x2
Now square the numbers
16 + 9 = x2
Add to get
25 = x2
Finally, find a positive number whose square is 25.
x = 5
Now try one by yourself. If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.
Exercise 1
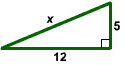
Consider the right triangle shown below. Find the value of x.
Answer
![]()
Sometimes on the CAHSEE, the problem will give the lengths of one leg and the hypotenuse of a right triangle. The problem will ask you to find the third leg. Here is an example.
Example 2
Consider the right triangle shown below. Find the value of x.
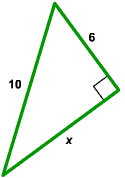
Solution
First notice that the length of the two legs are x and 6. The length of the hypotenuse is 10. Using the letters from the Pythagorean Theorem, we have
a = x
b = 6
c = 10
Now we use the Pythagorean Theorem
a2 + b2 = c2
or
x2 + 62 = 102
Now square the numbers
x2 + 36 = 100
Subtract to get
x2 = 100 - 36
= 64
Finally, find a positive number whose square is 64.
x = 8
Now try one by yourself. If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.
Exercise 2
Consider the right triangle shown below. Find the value of x.
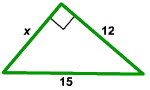
Answer
![]()
Example 3
A cell phone company advertises that length of their rectangular screen (between opposite corners) is 5 inches. The height of the screen is 4 inches. What is the width of the screen?
Solution
A diagram of the cell phone screen is shown below
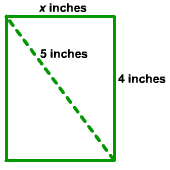
The top part forms a right triangle with the length of the two legs x and 4. The length of the hypotenuse is 5. Using the letters from the Pythagorean Theorem, we have
a = x
b = 4
c = 5
Now we use the Pythagorean Theorem
a2 + b2 = c2
or
x2 + 42 = 52
Now square the numbers
x2 + 16 = 25
Subtract to get
x2 = 25 - 16
= 9
Finally, find a positive number whose square is 9.
x = 3
The width of the screen is 3 inches.
Now try one by yourself. If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.
Exercise 3
Three players were playing catch. The first threw the ball 30 feet due north to the second player. The second player then threw the ball 40 feet due east to the third player. The third player threw the ball back to the first player. Use the diagram below to determine how far the third player threw the ball.
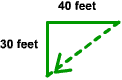
Answer
![]()