Inverses
Inverses
|
Definition The inverse of a relation R is the relation consisting of all ordered pairs (y,x) such that (x,y) belongs to R |
Example:
The inverse of the relation
(2,3), (4,5), (2,6), (4,6)
is
(3,2), (5,4), (6,2), (6,4)
Generally we switch the roles of x and y to find the inverse.
For functions, we follow the steps below to find the inverse:
-
Step 1: Switch the x and y.
-
Step 2: Solve for y.
-
Step 3: Write in inverse notation.
Example
Find the inverse of
y = 2x + 1
Solution
-
We write
x = 2y + 1
-
We solve:
x - 1 = 2y
x - 1
y =
2
-
We write
x - 1
f -1(x) =
2
Notice that the original function took x, multiplied by 2 and added 1, while the inverse function took x, subtracted 1 and divided by 2. The inverse function does the reverse of the original function in reverse order.
Exercises
Find the inverse of
-
x - 1
f(x) =
x + 1

-
f(x) = 3x3 - 2

-
f(x) = 3x - 4

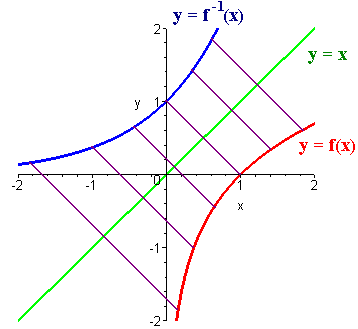
Graphing Inverses
To graph an inverse we imaging folding the paper across the y = x line and copy where the ink smeared in the other side.
One to One Functions
A function y = f(x) is called one to one if for every y value there is only one x value with y = f(x). That is, each y value comes from a unique x value.
Example
-
Determine if
y = 2x - 3
is one to one
Solution
For any two values a and b if
y = 2a - 3
and
y = 2b - 3
then
2a - 3 = 2b - 3
2a = 2b
a = b
Hence this function is 1-1.
-
Determine if
y = x2
is one to one
Solution
Now if
a2 = b2
then
a =
 b
b
In particular
a = -b
is a viable solution, for example
12 = (-1)2
hence this function is not 1-1.
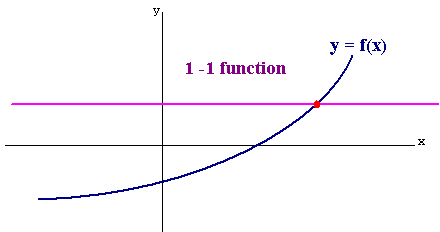
The Horizontal Line Test
If the graph of a function is such that every horizontal line passes through the graph at at most one point then the function is 1-1.
The graph below is the graph of a 1 -1 function since every horizontal line crosses the graph at most once.
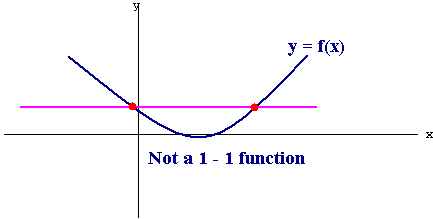
However, the graph below is not the graph of a 1 -1 function, since there is a horizontal line that crosses the graph more than once.
|
Theorem
If a function is 1-1, then its inverse is also a function |
An application of this is if we want a computer to find an inverse function, then we first have the computer check to see if the function is one to one, then have it proceed to find the inverse.
Back to the Functions Home Page
Back to the Intermediate Algebra (Math 154) Home Page