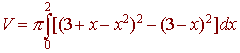Please work out each of the
given problems. Credit will be
based on the steps that you show towards the final answer. Show your work.
PROBLEM 1 Integrate the following functions
A)
![]()
Solution
u = ln(2x) du =
1/x dx from
2(1/2x)
dv =
x v = x2
/ 2
The integration by parts formula gives
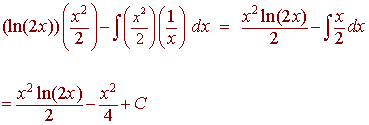
Solution
For this integral, we use substitution with
u = 1 - x du = -dx x = 1 - u 1 + x = 2 - u
This gives
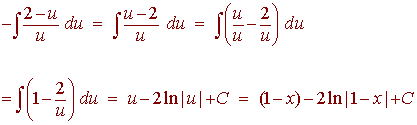
Solution
u = 5x5 - 3 du = 25x4
This gives
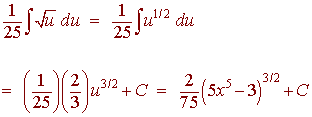
PROBLEM 2 Find the area of the region bounded by the curve
y = x3 - 3x2 - 4x
and the line
y = 6x
Solution
We first sketch the graph of the region
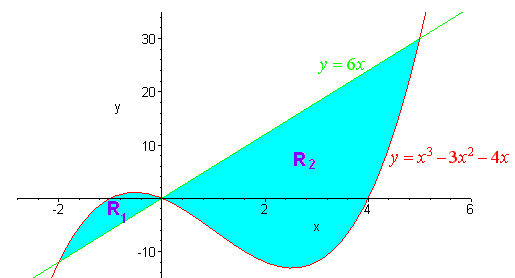
We can see that we will need to do two integrals since on the left (R1) the top curve is the cubic and the bottom curve is the line and on the right hand side (R2) the top curve is the line and bottom is the cubic. From the graph it appears that the equations intersect at -2, 0, and 5. Let's verify this. We set the equations equal to each other.
x3 - 3x2 - 4x = 6x x3 - 3x2 - 10x = 0
x(x2 - 3x - 10) = 0 x(x + 2)(x - 5) = 0
As we guessed the intersection points are at -2, 0, and 5. Now we integrate
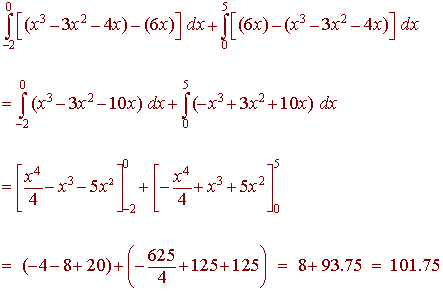
PROBLEM 3 Approximate the following integral using the midpoint rule with n = 4.
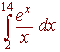
We first calculate
b - a 14
- 2
Dx
=
=
= 3
n
4
The we get the four rectangles with left and right endpoints
[2,5], [5,8], [8,11], [11,14]
The midpoints of these rectangles are
3.5, 6.5, 8.5, and 12.5
Now we use the midpoint rule. The integral can be approximated by
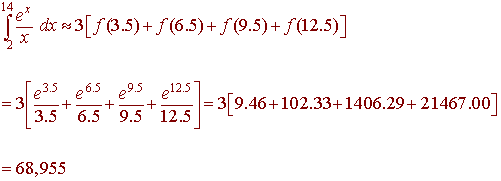
PROBLEM 4
The revenue R in
thousands of dollars at time t years after 1990
of a travel agency can be modeled by the equation
R(t) = t2 + t e-t
. Find the total revenue of the
company from 1990 to 2000.
Solution
The total revenue is the integral
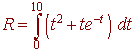
We use integration to integrate the second term
u = t dv = e-t
du = dt
v = -e-t
This gives us
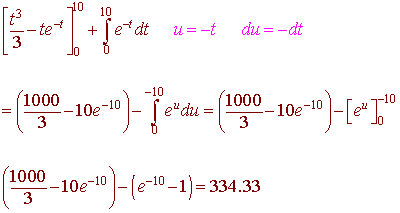
PROBLEM 5 Set up the integral to find the volume of the solid that results when the region bounded by the curves
y = 3 - x and y = 3 + x - x2
is revolved about the x-axis. You do not need to evaluate the integral.
We first sketch the graph. Then draw a cross-section and revolve it about the x-axis.
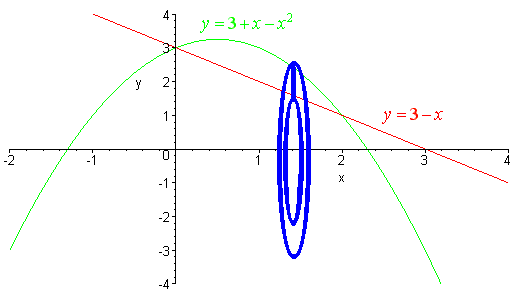
We see that the cross-section is a washer with larger and smaller radii
R = 3 + x - x2 and r = 3 - x
The area of the cross-section is
A = p(R2 - r2) = p[(3 + x - x2)2 - (3 - x)2]
The curves appear to intersect at 0 and 2. We solve to make sure of this.
3 + x - x2 = 3 - x x2 - 2x = 0
x(x- 2) = 0
and they do intersect at 0 and 2. Putting this together gives